Bạn đã từng mất ngủ khi tìm cách tốt nhất để đầu tư kinh doanh đạt tối đa hóa lợi nhuận và giảm thiểu rủi ro? Đừng trằn trọc nữa
Bạn đã từng mất ngủ khi tìm cách tốt nhất để đầu tư kinh doanh đạt tối đa hóa lợi nhuận và giảm thiểu rủi ro? Đừng trằn trọc nữa. Hãy thư giãn và dễ dàng ứng phó dù bất cứ chuyện gì xảy ra chăng nữa.
Tiền mặt, đúng thế. Hãy xem dòng tiền mặt của bạn, hay những gì sẽ đi vào và đi ra khỏi doanh nghiệp của bạn. Dòng tiền dương là số đo của tiền mặt chảy vào (tiền bán hàng, tiền lãi suất thu được, tiền phát hành cổ phần, v.v…), trong khi dòng tiền âm là số đo của tiền mặt chảy ra (tiền mua hàng, tiền lương, tiền thuế, v.v…). Dòng tiền ròng là sự chênh lệch giữa dòng tiền âm và dòng tiền dương của bạn, là câu trả lời cốt lõi nhất cho vấn đề kinh doanh: Bạn thu lại bao nhiều tiền lợi nhuận cuối kỳ?
Để phát triển kinh doanh, bạn cần phải đưa ra các quyết định then chốt, tiền của bạn sẽ đầu tư về đâu trong dài hạn. Microsoft Excel có thể giúp bạn so sánh các tùy chọn và đưa ra các quyết định đúng đắn, vì vậy bạn có thể thư giãn nghỉ ngơi cả ngày lẫn đêm.
Đặt câu hỏi về các dự án đầu tư vốn
Nếu bạn muốn số tiền được thu về nhiều hơn ở cuối kỳ, hãy để tiền đó trở thành vốn lưu động và đầu tư trong những dự án phát triển doanh nghiệp của bạn, bạn cần phải tìm hiểu về các dự án đó thông qua các câu hỏi như sau:
- Dự án dài hạn mới có khả năng sinh lợi không? Khi nào?
- Có phải tiền sẽ được đầu tư tốt hơn vào một dự án khác không?
- Tôi có nên đầu tư nhiều hơn trong các dự án đang đầu tư hay đã đến lúc cắt các khoản thua lỗ?
Bây giờ hãy xem xét kỹ hơn từng dự án đó và hỏi:
- Dòng tiền dương và dòng tiền âm của dự án này là những khoản nào?
- Đầu tư ban đầu có tác động lớn gì và bao nhiêu là quá nhiều?
Cuối cùng, những gì bạn thực sự cần là mấu chốt mà bạn có thể sử dụng để so sánh lựa chọn các dự án. Nhưng để đạt được điều đó, bạn phải kết hợp giá trị thời gian của đồng tiền vào các phân tích của bạn.
Một lần bố nói với tôi, "Con trai, sẽ tốt hơn nếu con có được tiền càng sớm càng tốt và hãy giữ nó càng lâu càng tốt." Sau này, tôi đã hiểu tại sao. Bạn có thể đầu tư khoản tiền này ở mức lãi kép, có nghĩa là tiền của bạn có thể mang lại cho bạn nhiều tiền hơn — và thậm chí còn nhiều hơn nữa. Nói cách khác, thời điểm tiền mặt chảy ra hay chảy vào cũng quan trọng như số tiền lưu chuyển là bao nhiêu.
Trả lời câu hỏi bằng việc sử dụng NPV và IRR
Có hai phương pháp tài chính mà bạn có thể sử dụng để giúp bạn trả lời tất cả những câu hỏi này: giá trị hiện tại ròng (NPV) và tỷ suất sinh lợi nội tại (IRR). Cả NPV và IRR đều được gọi là các phương pháp dòng tiền được chiết khấu bởi chúng đưa giá trị thời gian của đồng tiền làm một yếu tố trong đánh giá dự án đầu tư vốn của bạn. Cả NPV và IRR đều được dựa trên một chuỗi các khoản thanh toán (dòng tiền âm), thu nhập (dòng tiền dương), lỗ (dòng tiền âm) hay "không có lãi" (dòng tiền bằng không) trong tương lai.
NPV
NPV trả về giá trị ròng của các dòng tiền — được biểu thị bằng giá trị tiền của ngày hôm nay. Do giá trị theo thời gian của tiền, nhận một đô-la vào ngày hôm nay có giá trị nhiều hơn nhận một đô-la vào ngày mai. NPV tính giá trị hiện tại cho từng chuỗi dòng tiền mặt và cộng chúng lại với nhau để có được giá trị hiện tại ròng.
Công thức tính NPV như sau:
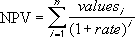
Trong đó, n là số dòng tiền và i là lãi suất hoặc tỷ lệ chiết khấu.
IRR
IRR được dựa trên NPV. Bạn có thể nghĩ nó như là một trường hợp đặc biệt của NPV, trong đó mức lãi được tính là lãi suất tương ứng với giá trị hiện tại ròng bằng 0 (không).
NPV(IRR(values),values) = 0
Khi tất các dòng tiền âm xảy ra sớm hơn tất cả các dòng tiền dương trong quy trình, hoặc khi chuỗi các dòng tiền của dự án chỉ chứa duy nhất một dòng tiền âm, IRR trả về một giá trị duy nhất. Hầu hết các dự án đầu tư vốn bắt đầu với một dòng tiền âm lớn (đầu tư trước) tiếp theo là một chuỗi các dòng tiền dương, do đó các dự án này luôn có một IRR duy nhất. Tuy nhiên, đôi khi sẽ có nhiều hơn một IRR có thể chấp nhận được, hoặc không có gì cả.
So sánh các dự án
NPV xác định một dự án sẽ kiếm được nhiều hay ít hơn tỷ lệ lợi nhuận mong muốn (còn gọi là tỷ lệ rào cản) và rất tốt trong việc tính ra liệu dự án đó có khả năng sinh lợi hay không. IRR đi xa hơn một bước so với NPV trong việc xác định tỷ lệ lợi nhuận cho một dự án cụ thể. Cả NPV và IRR cung cấp các số mà bạn có thể sử dụng để so sánh các dự án cạnh tranh và lựa chọn quyết định tốt nhất cho doanh nghiệp của bạn.
Chọn hàm Excel thích hợp
Bạn có thể sử dụng hàm Office Excel nào để tính NPV và IRR? Có năm hàm: hàm NPV, hàm XNPV, hàm IRR, hàm XIRR và hàm MIRR. Lựa chọn hàm nào tùy theo phương pháp tài chính bạn ưu tiên, dòng tiền có xảy ra ở các khoảng thời gian thường xuyên hay không và dòng tiền có định kỳ hay không.
Lưu ý: Dòng tiền được xác định bởi giá trị âm, dương hoặc bằng không. Khi bạn sử dụng các hàm này, hãy đặc biệt chú ý xử lý dòng tiền trực tiếp xảy ra ở giai đoạn đầu của chu kỳ đầu tiên và tất cả các dòng tiền khác đều xảy ra vào lúc kết thúc chu kỳ.
| Cú pháp hàm | Sử dụng khi bạn muốn | Chú thích |
|---|
| Hàm NPV (tỷ_lệ; giá_trị_1; [giá_trị_2]; …) | Xác định giá trị hiện tại ròng bằng cách dùng dòng tiền xảy ra ở các khoảng thời gian thường xuyên, chẳng hạn như hàng tháng hoặc hàng năm. | Mỗi dòng tiền, được xác định là một giá trị, xảy ra vào cuối chu kỳ.Nếu có một dòng tiền bổ sung ở đầu chu kỳ đầu tiên, nó sẽ được thêm vào giá trị trả về hàm NPV. Hãy xem ví dụ 2 trong chủ đề trợ giúp hàm NPV . |
| Hàm XNPV (tỷ_lệ, giá_trị, ngày) | Xác định giá trị hiện tại ròng bằng cách dùng dòng tiền xảy ra ở các khoảng thời gian không thường xuyên. | Mỗi dòng tiền, được xác định là một giá trị, xảy ra vào ngày thanh toán đã dự kiến. |
| Hàm IRR (giá_trị; [ước_đoán]) | Xác định suất sinh lợi nội tại bằng cách dùng dòng tiền xảy ra ở các khoảng thời gian thường xuyên, chẳng hạn như hàng tháng hoặc hàng năm. | Mỗi dòng tiền, được xác định là một giá trị, xảy ra vào cuối chu kỳ.IRR được tính toán thông qua một thủ tục tìm kiếm lặp bắt đầu với một ước tính cho IRR – được xác định là một lần đoán — và sau đó liên tục thay đổi giá trị đó cho đến khi đạt được một IRR chính xác. Việc xác định đối số đoán là tùy chọn; Excel sử dụng 10% là giá trị mặc định.Nếu có hơn một câu trả lời có thể chấp nhận, hàm IRR chỉ trả về kết quả đầu tiên tìm được. Nếu IRR không tìm thấy bất kỳ câu trả lời nào, nó trả về giá trị lỗi #NUM! giá trị lỗi. Sử dụng một giá trị khác cho lần đoán nếu bạn gặp lỗi hoặc kết quả không như bạn mong đợi.Chú ý Một lần đoán khác có thể trả về một kết quả khác nếu có nhiều hơn một tỷ suất sinh lợi nội tại. |
| Hàm XIRR (giá_trị; ngày; [ước_đoán]) | Xác định suất sinh lợi nội tại bằng cách dùng dòng tiền xảy ra ở các khoảng thời gian không thường xuyên. | Mỗi dòng tiền, được xác định là một giá trị, xảy ra vào ngày thanh toán đã dự kiến.XIRR được tính toán thông qua một quy trình tìm kiếm lặp bắt đầu với một ước tính cho IRR – được xác định là một lần đoán — và sau đó liên tục thay đổi giá trị đó cho đến khi đạt được một XIRR chính xác. Việc xác định đối số đoán là tùy chọn; Excel sử dụng 10% là giá trị mặc định.Nếu có hơn một câu trả lời có thể chấp nhận, hàm XIRR chỉ trả về kết quả đầu tiên tìm được. Nếu XIRR không tìm thấy bất kỳ câu trả lời nào, nó trả về giá trị lỗi #NUM! giá trị lỗi. Sử dụng một giá trị khác cho lần đoán nếu bạn gặp lỗi hoặc kết quả không như bạn mong đợi.Chú ý Một lần đoán khác có thể trả về một kết quả khác nếu có nhiều hơn một tỷ suất sinh lợi nội tại. |
| Hàm MIRR (giá_trị; tỷ_lệ_tài_chính; tỷ_lệ_tái_đầu_tư) | Xác định suất sinh lợi nội tại đã sửa đổi bằng cách dùng dòng tiền xảy ra ở các khoảng thời gian thường xuyên, chẳng hạn như hàng tháng hay hàng năm và xem xét cả chi phí đầu tư và lãi nhận được khi tái đầu tư tiền mặt. | Mỗi dòng tiền, được xác định là một giá trị, xảy ra vào cuối kỳ, ngoại trừ dòng tiền đầu tiên được xác định là một giá trị vào giai đoạn đầu của chu kỳ.Lãi suất bạn trả cho số tiền đó được dùng trong dòng tiền được xác định trong lãi suất tài chính. Lãi suất bạn nhận được từ dòng tiền khi tái đầu tư chúng được xác định trong lãi suất tái đầu tư. |